✔︎ 도함수의 응용
함수 𝑓가 구간 𝐼에서 정의되어 있을 때, 𝐼 내의 𝒙₁ <𝒙₂인 임의의 두 점 𝒙₁, 𝒙₂에 대하여 𝑓(𝒙₁)<𝑓(𝒙₂)를 만족하면 𝑓는 구간 𝐼에서 증가(increasing)한다고 하며, 𝒙₁ <𝒙₂인 𝐼 내의 임의의 두 점 𝒙₁, 𝒙₂에 대하여 𝑓(𝒙₁)>𝑓(𝒙₂)를 만족하면 𝑓는 구간 𝐼에서 감소(decreasing)한다고 한다. 도함수는 다음과 같이 함수가 증가하거나 감소하는 상황을 알려준다.
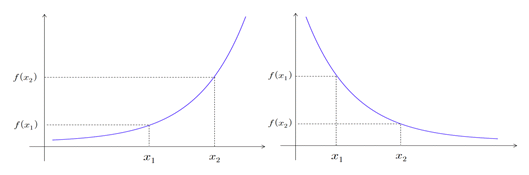
함수 𝑓가 폐구간 [a, b]에서 연속이고 개구간 (a, b)에서 미분가능하다고 하자. 그러면 다음이 성립한다.
① 구간 (a, b)내의 모든 점에서 𝑓 '(𝒙) > 0 이면, 𝑓는 [a, b]에서 증가한다.
② 구간 (a, b)내의 모든 점에서 𝑓 '(𝒙) < 0 이면, 𝑓는 [a, b]에서 감소한다.
예를 들어, 𝑓 '(c) > 0 이면 𝒙 = c 에서의 접선의 기울기가 양수이므로, 𝒙 = c 의 근방에서는 함수가 증가함을 알 수 있다.
마찬가지로 𝑓 '(c) < 0 이면 𝒙 = c 의 근방에서는 함수가 감소함을 알 수 있다.

예제 1. 함수 𝑓(𝒙) = 𝒙³-6𝒙²+9𝒙+1이 증가하는 구간과 감소하는 구간을 구하시오.
f(x) = x^3 - 6*x^2 + 9*x + 1
df(x) = diff(f(x), x)
p = plot(f(x), (x, -1, 4), ymin = -5) # 함수의 그래프
show(p)
print("f'(x) = ", df(x)) # 도함수
solve(df(x) > 0, x) # 도함수가 0보다 크게 되는 x값의 범위
따라서 함수는 𝒙 < 1, 𝒙 > 3일 때 증가, 1 < 𝒙 < 3 일 때 감소한다.
✔︎ 2계 도함수의 응용
함수 𝑓가 𝒙 = c에서 미분가능하고 (c, 𝑓(c))가 곡선 𝒚 = 𝑓(𝒙) 위의 점이라 할 때, 점 c를 포함하는 적당한 개구간 𝐼가 존재하여 𝒙 ≠ c 인 구간 𝐼의 각 점 𝒙에 대응하는 곡선 위의 모든 점 (𝒙. 𝑓(𝒙))가 점 (c. 𝑓(c))에서의 접선 아래쪽에 있으면 곡선 𝒚 = 𝑓(𝒙)는 점 (c. 𝑓(c))에서 위로 볼록 또는 아래로 오목하다고 하고, 반대로 접선의 위쪽에 있으면 아래로 볼록 또는 위로 오목하다고 한다.
또, 곡선 𝒚 = 𝑓(𝒙)가 점 𝒙 = c에서 연속일 때 (𝑓 '(c))는 존재하지 않아도 무방함), 곡선 위의 점 (c, 𝑓(c))를 경계로 한쪽에서는 위로 볼록하고 다른 쪽에서는 아래로 볼록할 때, (c. 𝑓(c))를 곡선 𝒚 = 𝑓(𝒙)의 변곡점이라 한다. 2계 도함수는 다음과 같이 함수가 위로 볼록하거나 아래로 볼록하는 상황을 알려준다.

함수 𝑓가 점 c를 포함하는 적당한 개구간 𝐼에서 미분가능하고 𝑓 ''(c)가 존재할 때, 다음이 성립한다.
① 𝑓 ''(c) > 0 이면, 곡선 𝑓는 점 (c, 𝑓(c)) 에서 아래로 볼록하다.
② 𝑓 ''(c) < 0 이면, 곡선 𝑓는 점 (c, 𝑓(c)) 에서 위로 볼록하다.
𝑓 ''(c) > 0 이면 𝑓 '' = (𝑓 ')' 이므로 𝑓 ' 는 𝒙 = c 의 근방에서 증가함을 알 수 있고, 𝑓 '은 접선의 기울기를 의미하므로, 접선의 기울기가 증가하는 상황이다. 따라서 다음 그림과 같이 아래로 볼록임을 알 수 있다. 마찬가지로 𝑓 ''(c) < 0 이면 접선의 기울기가 감소하므로 위로 볼록임을 알 수 있다.

예제 2. 함수 𝑓(𝒙) = ⅓𝒙³-𝒙²-3𝒙+4는 어디에서 위로 볼록하고. 아래로 볼록한지 판단하시오.
f(x) = 1/3*x^3 - x^2 - 3*x + 4
df(x) = diff(f(x), x) # 도함수
d2f(x) = diff(df(x), x) # 2계 도함수
p = plot(f(x), (x, -3, 5), ymin = -5) # 함수의 그래프
show(p)
print("f''(x) = ", d2f(x)) # 2계 도함수
solve(d2f(x) > 0, x) # 2계 도함수가 0보다 큰 x값의 범위
# 1보다 큰 범위에서 함수가 아래로 볼록
따라서 𝒙 < 1 에서 위로 볼록이고, 𝒙 > 1 에서 아래로 볼록이다. (1, ⅓)은 변곡점이다.
✔︎ 극대, 극소, 최대, 최소
𝑓(𝒙)가 폐구간 [a, b] 에서 연속이면 이 구간에서 𝑓(𝒙)가 최댓값을 취하는 점 및 최솟값을 취하는 점이 존재한다. 함수 𝑓 가 𝒙 = c 의 근방의 모든 점 𝒙에 대하여 𝑓(𝒙) ≤ 𝑓(c) 가 성립하면 함수 𝑓 는 𝒙 = c 에서 극댓값 𝑓(c)를 갖는다. 반대로 함수 𝑓 가 𝒙 = c 의 근방의 모든 점 𝒙에 대하여 𝑓(𝒙) ≥ 𝑓(c) 가 성립하면 함수 𝑓 는 𝒙 = c 에서 극솟값 𝑓(c)를 갖는다. 또, 𝑓 의 극댓값과 극솟값을 통틀어 극값이라 하고, 극대점 또는 극소점 (c, 𝑓(c))를 극점(extreme point)이라 한다.

극값이 생길 수 있는 후보들은 𝑓 '(c) = 0 이거나 𝑓 '(c)가 존재하지 않는 점 𝒙 = c 이다. 함수의 미분계수가 0이거나 존재하지 않는 점을 함수의 임계점(critical point)이라고 한다.
[Fermat의 임계점 정리]
함수 𝑓 가 개구간 (a, b)에서 연속이고 𝒙 = c(∈(a, b))에서 극값을 갖는다면, 𝑓 '(c) = 0 이거나 𝑓 '(c)가 존재하지 않는다.
예제 3. 함수 𝑓(𝒙) = -2𝒙³+3𝒙²의 임계점을 구하시오.
𝑓 ' = -6𝒙²+6𝒙 = 0에서 임계점은 𝒙 = 0 또는 𝒙 = 1 이다.
f(x) = -2*x^3 + 3*x^2
df(x) = diff(f(x), x)
solve(df(x) == 0, x)[x == 0, x == 1]
도함수를 이용하면 극댓값과 극솟값을 쉽게 판정할 수 있다. 함수 𝑓 가 정의역 내의 한 점 c 에서 𝑓 '과 𝑓 ''을 가지며, 𝑓 '(c) =0일 때,
① 𝑓 ''(c) < 0이면, 𝑓 (c)는 함수 𝑓 의 극댓값이다.
② 𝑓 ''(c) > 0이면, 𝑓 (c)는 함수 𝑓 의 극솟값이다.
𝑓 ''(c) < 0이면 점 (c, 𝑓(c))에서 위로 볼록인데, 𝑓 '(c) =0 이므로 다음 그림에서 𝑓 (c)는 함수 𝑓 의 극댓값임을 쉽게 알 수 있다. 마찬가지로 𝑓 ''(c) > 0이면 아래로 볼록이므로 𝑓 (c)는 함수 𝑓 의 극솟값임을 알 수 있다.

폐구간에서 연속인 함수 𝑓의 최댓값과 최솟값은 임계점에서의 함숫값과 구간의 양 끝점에서의 함숫값을 비교하여 구하면 된다.
[1 단계] 구간 𝐼 에서 𝑓 의 임계점들을 찾는다.
[2 단계] 이 각각의 임계점들과 양 끝점에서 𝑓 의 값을 계산한다. 그 중 가장 큰 값이 최댓값이고, 가장 작은 값이 최솟값이다.
예제 4. 함수 𝑓(𝒙) = ⅓𝒙³-𝒙²-3𝒙+4가 구간 [-2. 6]에서 정의되었다고 할 때, 𝑓의 극댓값과 극솟값을 구하라. 또, 𝑓의 최댓값과 최솟값을 구하라.
f(x) = 1/3*x^3 - x^2 - 3*x + 4
df(x) = diff(f(x), x)
d2f(x) = diff(df(x), x)
solve(diff(f(x)) == 0, x) # 여기까지 실행하면 [x == 3, x == -1]을 얻음
print(d2f(3), d2f(-1)) # 3일 때 극댓값, -1일 때 극솟값
print("극댓값 =", f(3))
print("극솟값 =", f(-1))
print(f(-2), f(6)) # 구간의 양 끝점에서의 함숫값과 비교
-4 4
극댓값 = 17/3
극솟값 = -5
10/3 22
따라서 극댓값은 17/3, 극솟값은 -5, 최댓값은 22, 최솟값은 -5 이다.
'◦ Machine Learning > Mathmatics' 카테고리의 다른 글
| [기초수학] 순열과 조합, 확률, 확률변수, 확률분포, 베이지안 (0) | 2021.01.17 |
|---|---|
| [기초수학] 경사하강법과 최소제곱문제의 해 (1) | 2021.01.16 |
| [기초수학] 극한과 도함수 (0) | 2021.01.11 |
| [기초수학] 정사영과 최소제곱문제 (0) | 2021.01.09 |
| [기초수학] 선형연립방정식의 해집합 (0) | 2021.01.08 |