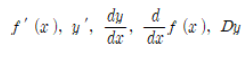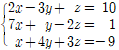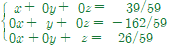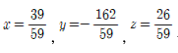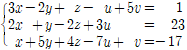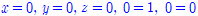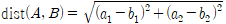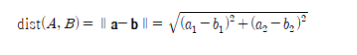MINJU's code story

✔︎ 순열과 조합

- 순열(permutation): 순서를 고려하여 나열하는 경우의 수

• nPk : 서로 다른 n개에서 k개를 택하여 순서대로 나열한 순열의 수
• nPk = n(n-1)…(n-k+1) (k≤n)
• k = n 일 때 nPn = n(n-1)…2•1 = n!

예제 1. 1부터 9까지의 숫자 중에서 서로 다른 3개를 선택하여 3자리 수를 만들려고 한다. 만들 수 있는 자연수의 개수를 구하시오.

풀이) ₉P₃ = 9 x 8 x 7 = 504

factorial(9)/factorial(6)

504

- 조합(combination): 순서와 상관없이 선택하는 경우의 수

• 예를 들어, 1, 2, 3, 4, 5가 적힌 5장의 카드에서 세 장을 택하는 경우의 수는 5x4x3 / 3! = 10 이다.
• nCk : 서로 다른 n개에서 k개를 택하는 조합의 수  

예제 2.  500개의 넥타이로부터 5개의 넥타이를 택하는 방법의 개수

factorial(500)/(factorial(5)*factorial(495))

binomial(500, 5)  # binomial(n, k)  서로 다른 n개에서 k개를 택하는 조합의 수

255244687600

- 만일 중복을 허락한다면 다음과 같이 중복순열과 중복조합을 계산할 수 있다.

• 중복순열(repeated permutation): 서로 다른 n개에서 중복을 허용하여 k개를 택하여 순서대로 나열한 경우의 수

• 중복조합(repeated combination): 서로 다른 n개에서 중복을 허용하여 (순서없이) k개를 택하는 경우의 수

예제 3. 숫자 1, 2, 3, 4, 5 중에서 중복을 허락하여 세 개를 택해 일렬로 나열하여 만든 세 자리의 자연수가 5의 배수인 경우의 수를 구하시오.

풀이) 일의 자리를 5로 고정시키면 되므로, 나머지 두 자리를 1, 2, 3, 4, 5 중에서 중복을 허락하여 나열하는 경우의 수와 같다. 따라서 다음을 얻는다.

예제 4. 4명의 사람이 A, B, C 중 한 명에게 무기명으로 투표를 할 때, 나올 수 있는 경우의 수를 구하시오.

풀이) 4명이 무기명으로 투표하는 방법은 AAAA, AAAB, ..., BCCC, CCCC 이므로

✔︎ 확률

- 확률(probability): 특정 사건(event)이 일어날 가능성을 0과 1 사이의 값으로 나타낸 것

• 확률이 0: 사건이 절대로 일어날 수 없음, 확률이 1: 사건이 반드시 일어남.
• 표본공간(Sample Space): 사건들의 집합.
• 예를 들어, 동전 던지기의 경우 발생가능한 사건들은 {앞면, 뒷면} 으로 나타낼 수 있으며, 정육면체 주사위의 경우 {1, 2, 3, 4, 5, 6} 으로 나타낼 수 있다.
• S를 전체 사건의 집합(표본공간)이라 하고, A를 특정 사건의 집합이라 하자. 그러면 사건 A가 일어나는 가능성을 수로 나타낸 확률 P(A)는 A가 일어나는 경우의 수 n(A)를 전체 경우의 수 n(S)로 나누어서 구한다.

(1) 수학적 확률

(2) 기하학적 확률

(3) 통계적 확률과 대수의 법칙(Law of large number)

n번의 시행 동안, 특정 사건 A가 일어난 횟수가 k번이면, A의 통계적 확률을 k/n라 말할 수 있다. 그러나 시행 횟수 n이 충분히 커지면 통계적 확률은 수학적 확률과 같아진다.

확률은 다음 성질을 만족한다. 사건 A의 확률을 P(A)라 하면

① 표본공간 S에서 임의의 사건 A에 대하여 0 ≤ P(A) ≤ 1

② 표본공간 S에 대하여 P(S) = 1 (표본공간 전체의 확률은 1)

③ 공사건 ⦰에 대하여 P(⦰) = 0

④ 두 사건 A, B가 동시에 발생하지 않는 배반사건이면 P(A∪B) = P(A) + P(B)

⑤ 사건 A가 일어나지 않는 경우를 A 여집합이라고 하면

예제 5.  박스 안에 빨간 공 6개와 파란 공 4개가 들어 있다. 처음 빨간 공을 꺼내고, 두 번째 파란 공을 꺼낼 확률은 다음과 같다.

factorial(6)*factorial(4)/factorial(10)

1/210

예제 6. R 명령어로 동전 한 개를 10회 던져 보고, 뒷면의 수와 앞면의 수를 기록해 보자.

coin = sample(c("뒤","앞"), 10, replace = TRUE)   # 10회 반복 
coin

[1] "뒤" "뒤" "뒤" "앞" "뒤" "뒤" "앞" "뒤" "뒤" "뒤"

위의 코드에서 coin 대신에 table(coin) 명령어를 사용하면 다음과 같이 표로 나타내준다.

coin = sample(c("뒷면","앞면"), 100, replace = TRUE)   # 10회 반복 
table(coin)

coin
뒷면 앞면
54 46

*시행의 횟수를 아주 크게 늘려 가면, 앞서 대수의 법칙에서 설명한 바와 같이 뒷면과 앞면이 나오는 확률이 ½ (수학적 확률)로 수렴함을 확인할 수 있다.

예제 7. 1000개의 제품 중에 불량품이 3개 있다. 이 제품 중에서 10개의 제품을 구입했을 때 다음 확률을 구하시오.

(1) 구입제품 중 불량품이 한 개도 없는 경우

(2) 구입제품 중 불량품이 적어도 한 개 이상 있는 경우

풀이 1) 1000개의 제품 중에 10개의 제품을 선택하는 경우의 수는 ₁₀₀₀C₁₀. (1) 불량품이 한 개도 없는 경우는 정상 제품인 997개에서 10개를 모두 선택하고, 불량품 3개에서는 하나도 선택하지 않는 경우밖에 없으므로 그 경우의 수는 ₉₉₇C₁₀x₃C₀이다. R코드를 이용하여 계산하면 다음과 같다.

# 모두 불량품이 아닐 확률
choose(997, 10)* choose(3, 0)/ choose(1000, 10)

[1] 0.9702695

풀이 2) 불량품이 적어도 한 개 이상 있을 확률은, 1에서 불량품이 한 개도 없는 확률을 빼면 된다.

# 셀의 오른쪽 하단의 Language를 R로 변경하여 실행하세요.
# 적어도 불량품이 1개 이상 있을 확률
1 - choose(997, 10)*choose(3, 0)/choose(1000, 10)

[1] 0.02973045

✔︎ 조건부확률

- 어떤 사건 A가 일어났다는 조건 하에서 사건 B가 일어날 확률을 사건 A에 대한 사건 B의 조건부확률(conditional probability)이라고 한다.

- 곰셈정리(관계식)

- 일반적으로 사건 A₁, A₂, …, An에 대하여 다음이 성립한다.

✔︎ 베이즈 정리

- 베이즈 정리(Bayes’ theorem)는 주어진 조건에서 어떠한 현상이 실제로 나타날 확률을 구하는 방법으로, 불확실성 하에서 의사결정 문제를 수학적으로 다룰 때 중요하게 이용된다.

• 사전확률(prior probability)은 관측자가 이미 알고 있는 사건으로부터 나온 확률. P(A)는 A에 대한 사전확률.
• 사후확률(posteriori probability)은 어떤 특정사건이 이미 발생하였는데, 이 특정사건이 나온 이유가 무엇인지 불확실한 상황을 식으로 나타낸 것. P(A | B). 여기서 B는 이미 일어난 사건이고, 사건 B를 관측한 후에 그 원인이 되는 사건 A의 확률을 따졌다는 의미로 사후확률이라고 정의.
• 베이즈 정리는 사전확률과 사건으로부터 얻은 자료를 사용하여 사후확률을 추출해내는 것. 즉, 사전확률과 사후확률의 관계를 조건부 확률을 이용하여 계산하는 이론.

{A₁, A₂, …, An}이 표본공간 S의 분할(partition)을 이룬다고 하자. 그러면 임의의 사건 B에 대하여 다음이 성립한다.

이때 Aᵢ ⋂ B (𝑖 = 1, 2, …, n)는 서로 배반(exclusive)이다. 따라서

한편, 확률의 곱셈정리로부터 아레 전확률 공식(Law of Total Probability)을 얻을 수 있다.

또한, 임의의 𝑖에 대한 조건부확률 P(Aᵢ | B) = P(A⋂B) / P(B)에 P(Aᵢ | B) = P(Aᵢ)P(B | Aᵢ)와 전확률 공식을 대입하면 다음 식을 얻을 수 있는데 이를 베이즈 정리(Bayes' theorem)라고 한다.

여기서 P(Aᵢ)를 사건 Aᵢ의 사전확률, P(Aᵢ | B)를 사건 Aᵢ의 사후확률이라고 한다.

예제 8. 3대의 가계 A, B, C가 각각 이 공장의 생산품 전체의 50%, 30%, 20%를 생산한다. 그리고 이들 기계가 불량품을 생산할 비율은 각각 4%, 3%, 2%이다. 한 제품을 임의로 선택할 때 그 제품이 불량품일 확률을 구하여라. 또한 불량품이 가계 C에 의하여 생산될 확률을 구하시오.

풀이) 구입한 1개의 제품이 기계 C로 생산된 제품인 사건을 C로 나타내고, 그것이 불량품이라는 사건을 X로 나타내면,

- 제품을 생산하는 사건: A∪B∪C = S 이고, P(A) = 0.5, P(B) = 0.3, P(C) = 0.2

- 불량품을 생산하는 사건: X = (A⋂X)∪(B⋂X)∪(C⋂X)

- 불량품을 생산하는 확률: P(X | A) = 0.04, P(X | B) = 0.03, P(X | C) = 0.02

- 전확률 공식에 대입: P(X) = P(A)P(X | A) + P(B)P(X | B) + P(C)P(X | C) = 0.5x0.04+0.3x0.03+0.2x0.02 = 0.033

따라서 베이즈 정리에 의하여 불량품 중 기계 C가 생산한 제품이 불량품일 확률은 다음과 같다.

✔︎ 확률변수

- 어떤 값을 취하느냐가 확률적으로 결정되는 변수. 표본 공간의 모든 표본에 대해 어떤 실수 값을 대응시킨(할당한) 것.

✔︎ 이산확률분포

- 확률변수 X가 연속적이지 않은 값 𝒙₁, 𝒙₂, …, 𝒙n을 취할 때, X를 이산확률변수라고 하고, 각각의 𝒙ᵢ에 대하여 X = 𝒙ᵢ일 확률 P(X = 𝒙ᵢ)을 할당한 것을 이산확률분포라고 한다.

- 이산확률변수 X가 𝒙₁, 𝒙₂, …, 𝒙n의 값을 취할 때 확률 P(X = 𝒙ᵢ)을 대응시키는 함수 𝑓(𝒙)를 확률변수 X의 확률질량함수(probability mass function)라 한다.

- 확률질량함수는 다음과 같은 성질이 있다.

✔︎ 연속확률분포

- 확률변수 X가 어떤 범위에 속하는 모든 실수를 취할 때, X를 연속확률변수라 한다.

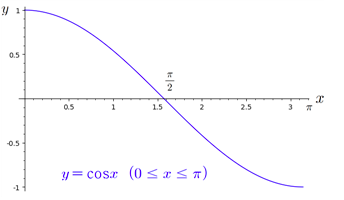
- 연속확률변수 X에 대하여 함수 𝑓(𝒙)가 다음의 성질을 만족하면 𝑓(𝒙)를 X의 확률밀도함수(probability density function)라 한다.

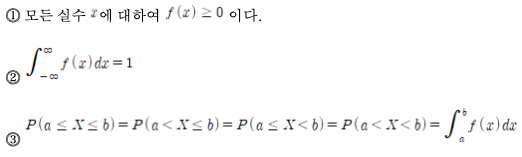
따라서 확률 P(a≤X≤b)는 아래 그림에서 색깔로 표시한 부분의 넓이와 같다. 이때 구간의 끝점(a, b)이 범위에 포함되는지의 여부는 관계가 없다.

✔︎ 경사하강법(Gradient Descent Algorithm)

경사하강법은 함수 𝑓 가 복잡하여 방정식을 풀어서 임계점을 구하는 것이 힘들 때 사용한다. 경사하강법의 기본 아이디어는 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 것이다.

[알고리즘]

[작동 원리]

우선 임의로 𝒙₁ 을 정하여 𝒈₁ = 𝑓 '(𝒙₁) 을 계산한다. 만일 |𝒈₁| ≤ ɛ (여기서 ɛ는 예를 들어, ɛ = 10⁻⁶ 과 같이 매우 작은 양수를 의미한다; epsilon)이 성립하면 𝑓 '(𝒙₁) ≈ 0 이 되어 (우리가 허용하는 오차범위에서) 임계점 정리를 만족하므로 알고리즘을 멈추고 𝒙₁ 을 최적인 근사해로 반환한다. 

그러나 |𝒈₁| > ɛ 이면 계산공식 𝒙₂ = 𝒙₁ - 𝜂𝒈₁ 을 이용하여 𝒙₂ 를 결정한다. 같은 방법으로 𝒈₂ = 𝑓 '(𝒙₂) 를 계산하여 임계점 정리를 만족하는지 판단해보고, 만일 성립되지 않으면 𝒙₃ 를 결정한다. 이런 방식으로 𝒙₄, 𝒙₅, … (→𝒙*)를 만들어 낸다.

아래 그림과 같이 𝒌번째 단계의 근사해 𝒙𝒌에서의 접선의 기울기가 𝐠𝒌 = 𝑓 '(𝒙𝒌) < 0 을 만족한다고 하자. 그러면 𝒙𝒌 에서 오른쪽으로(양의 방향) 이동할 때 함수가 감소하므로 최솟값을 갖는 최적해 𝒙*는 𝒙𝒌 의 오른쪽에 있다고 판단할 수 있다. 따라서 𝒙𝒌에서 -𝐠𝒌(>0) 방향(오른쪽)으로 이동하여 𝒙𝒌﹢₁ = 𝒙𝒌 - 𝜂𝒈𝒌 을 생성한다.

마찬가지로 아래 그림과 같이 𝒌번째 단계의 근사해 𝒙𝒌에서의 접선의 기울기가 𝐠𝒌 = 𝑓 '(𝒙𝒌) > 0 을 만족한다고 하자. 그러면 𝒙𝒌 에서 왼쪽으로(음의 방향) 이동할 때 함수가 감소하므로 최솟값을 갖는 최적해 𝒙*는 𝒙𝒌 의 왼쪽에 있다고 판단할 수 있다. 따라서 𝒙𝒌에서 -𝐠𝒌(<0) 방향(왼쪽)으로 이동하여 𝒙𝒌﹢₁ = 𝒙𝒌 - 𝜂𝒈𝒌 을 생성한다.

이를 통해 경사하강법은 𝑓(𝒙₁) > 𝑓(𝒙₂) > 𝑓(𝒙₃) …  가 만족되도록 𝒙₁, 𝒙₂, 𝒙₃, … 을 찾으려고 하는 것임을 알 수 있다. 이때 얼마만큼을 이동해야 하는지는 𝜂 (eta)가 결정하는데, 이를 학습률(learning rate)이라고 한다. 학습률이 너무 크면 𝒙*를 넘어서 지나칠 수 있고, 심지어 함수값이 증가하여 수렴하지 않을 수도 있다(아래 왼쪽 그림). 반대로 너무 작으면 수렴하는 속도가 느릴 수 있다(아래 오른쪽 그림). 

[참고]

적절한 학습률을 결정하는 것은 경사하강법에서 중요한 문제이나 여기서는 자세히 다루지 않는다. 학습률은 대개 10⁻⁶ 에서 1 사이의 범위에서 정하는 것으로 알려져 있으며, 초기 학습률로는 𝜂 = 0.1 또는 𝜂 = 00.1 이 주로 사용된다고 한다.

예제 1. 함수 𝑓(𝒙) = 2𝒙² - 3𝒙 +2 의 최솟값을 구하시오. 단, 𝒙₁ = 0, 𝜂 = 0.1, 𝒆 = 10⁻⁶ 으로 한다.

풀이) 𝑓 '(𝒙) = 4𝒙 -3 = 0 에서 임계점은 𝒙 = ¾ = 0.75 이고 𝑓(𝒙) 는 아래로 볼록한 이차함수이므로 𝒙 = ¾ 에서 최솟값 𝑓(¾) = ⅞ 임을 쉽게 알 수 있다.

f(x) = 2*x^2 - 3*x + 2  # 함수
df(x) = diff(f(x), x)  # 도함수
x0 = 0.0  # 초기 근사해
tol = 1e-6  # 허용오차
eta = 0.1  # 학습률

for k in range(300):
    
    g0 = df(x0)
    
    if abs(g0) <= tol:
        
        print("알고리즘 성공!")
        break
    
    x0 = x0 - eta*g0

print("x* =", x0)
print("|g*| =", abs(g0))
print("f(x*) =", f(x0))
print("반복 횟수 =", k + 1)

알고리즘 성공!
x* = 0.749999834194560
|g*| = 6.63221759289456e-7
f(x*) = 0.875000000000055
반복 횟수 = 31

위의 예제에서 경사하강법에 의해 생성된 점들 (𝒙₁, 𝑓(𝒙₁)), (𝒙₂, 𝑓(𝒙₂)), (𝒙₃, 𝑓(𝒙₃)), … 을 함수 𝐲 = 𝑓(𝒙) 의 그래프와 함께 좌표평면에 나타내면 다음과 같다. 그림을 통해 직관적으로 최솟값을 가지는 곡선위의 점 (𝒙*, 𝑓(𝒙*)) 에 수렴함을 쉽게 알 수 있다. 

경사하강법은 딥러닝에서 가중치를 업데이트하는 데 사용되는 핵심 알고리즘이기도 하다. 앞서 경사하강법을 소개할 때 정의역 전체에서 아래로 볼록(convex)인 함수를 가정하였다. 그러나 구간마다 아래로 볼록, 위로 볼록이 모두 포함된 함수(non-convex, 예. 아래 그림)에 경사하강법을 적용하면, 시작점 𝒙₁ 이 어디냐에 따라 서로 다른 극솟값 또는 (극대도 극소도 아닌) 임계점으로 수렴할 수도 있다.

✔︎ 응용(최소제곱문제)

최소제곱문제도 역시 경사하강법으로 해결할 수 있다.

min 𝑬(u)

다만 앞서 소개한 경사하강법은 독립변수가 하나인 일변수 함수 𝑓(𝒙)에 대하여 구성하였는데, 우리가 학습한 최소제곱문제는 독립변수가 최소 2개 이상인 다변수 함수 𝑬(u) 이므로 다음과 같이 변형된다.

[알고리즘]

다변수 함수에 대한 경사하강법도 기본적인 구성은 일변수 함수의 경우와 완전히 같으나 스칼라 𝒙 가 벡터 u로, 절대값 |𝐠| 가 벡터의 노름 ||𝐠|| 으로, 도함수 𝑓 '(𝒙) 가 (다변수함수에서 도함수 역할을 하는) 그래디언트(gradient) ∇𝑬(u) 로 바뀌는 것만 차이가 있다.

𝒙, 𝐲 를 독립적으로 변화하는 두 변수라 하고 𝐳 를 제 3의 변수라 하자. 𝒙, 𝐲 의 값이 각각 정해지면 여기에 대응하여 𝐳 의 값이 정해질 때 𝐳 를 두 변수 𝒙, 𝐲 의 함수라 하고 이것을 𝐳 = 𝑓(𝒙, 𝐲) 로 표시한다. 같은 방법으로 더 많은 변수의 함수도 정의할 수 있다. 이와 같이 이변수 이상의 함수를 일반적으로 다변수함수라 한다.

좌표 공간에서 𝒙, 𝐲 및 𝐳 = 𝑓(𝒙, 𝐲) 를 좌표로 하는 점 (𝒙, 𝐲, 𝐳)를 생각하고 𝒙, 𝐲를 움직이면 그들 점은 일반적으로 하나의 곡면을 이루게 되는데 이 곡면을 함수 𝐳 = 𝑓(𝒙, 𝐲) 의 그래프라 부른다.

var('x, y')  # 변수 정의
f(x, y) = -x*y*exp(-x^2 - y^2)
plot3d(f(x, y), (x, -2, 2), (y, -2, 2), opacity = 0.6, aspect_ratio = [1, 1, 10])

위의 그래프에서 산의 정상에 해당하는 부분에서 이변수 함수는 극댓값을 갖게 되고, 계곡의 바닥에 해당하는 부분에서 극솟값을 갖게 됨을 직관적으로 확인할 수 있다. 이 점을 찾기 위해서는 일변수 함수의 도함수에 해당하는 개념이 필요하다. 이를 다변수 함수의 그래디언트(gradient)라고 한다.

✔︎ 다변수 함수의 도함수(그래디언트)

이변수 함수 𝑓(𝒙, 𝐲) 의 그래디언트는 다음과 같이 정의된다.

여기서 𝜕𝑓 / 𝜕𝒙 는 𝑓 를 변수 𝒙 에 관하여 편미분한다는 뜻으로 𝒙 를 제외한 다른 변수는 모두 상수로 취급하여 미분하는 것과 같다. 

var('x, y')  # 변수 정의
f(x, y) = -x*y*exp(-x^2 - y^2)
f(x, y).gradient()  # 그래디언트

(2*x^2*y*e^(-x^2 - y^2) - y*e^(-x^2 - y^2), 2*x*y^2*e^(-x^2 - y^2) - x*e^(-x^2 - y^2))

같은 방법으로 독립변수가 3개 이상인 다변수함수 𝑓 에 대하여도 𝑓 의 그래디언트를 정의할 수 있다. 𝜂 변수 함수 𝑓(𝒙₁, 𝒙₂, …, 𝒙𝘯) 에 대하여 그래디언트는 다음과 같다.

각 데이터 (𝒙ᵢ, 𝐲ᵢ)에 대하여 𝒙ᵢ를 일차함수 𝐲 = a + b𝒙 에 대입하여 얻은 값을 ŷᵢ 라 하자(즉 ŷᵢ = a + b𝒙ᵢ). 이 선형연립방정식의 해가 존재하지 않는 경우. 각 데이터와 근사식 사이의 (제곱)오차 (𝐲ᵢ - ŷᵢ)² 가 최소가 되는 a, b를 구하기 위하여 각 데이터에 대하여 오차(error)를 더한 오차함수는 다음과 같다. (앞에 ½ 은 단지 계산의 편리성을 주기 위해서 곱해주었다.)

이에 대하여 경사하강법을 사용하면 다음을 얻는다. (u = (1, 1), 허용오차 ɛ = 10⁻⁶, 학습률 𝜂 = 0.1)

var('a, b')  # 변수 선언
# 오차함수
E(a, b) = 1/2*((a - 1)^2 + (a + b - 3)^2 + (a + 2*b - 4)^2 + (a + 3*b - 4)^2)
# 도함수(그래디언트)
gradE = E.gradient()
u = vector([1.0, 1.0])  # 초기 근사해
tol = 1e-6  # 허용오차 10^(-6)
eta = 0.1  # 학습률(learning rate)

for k in range(300):
    
    g = gradE(u[0], u[1])
    gn = g.norm()
              
    if gn <= tol:
        
        print("알고리즘 성공 !")
        break
    
    u = u - eta*g

print("u* =", u)
print("E(x*) =", E(u[0], u[1]))
print("반복 횟수 =", k + 1)

알고리즘 성공 !
u* = (1.49999931357138, 1.00000032150597)
E(x*) = 0.500000000000342
반복 횟수 = 106

따라서 최소제곱직선은 𝐲 = 3/2 + 𝒙 이다.

마찬가지로 𝒙, 𝐲 관계를 가장 잘 보여주는 이차식 𝐲 = a + b𝒙 + c𝒙² 도 찾을 수 있다. 오차는 다음과 같다. 

역시 경사하강법을 사용하면 아래의 이차함수 𝐲 = a + b𝒙 + c𝒙² 을 얻는다. (u = (1, 1, 1), 허용오차 ɛ = 10⁻⁶, 학습률 𝜂 = 0.01)

var('a, b, c')  # 변수 선언
# 오차함수
E(a, b, c) = 1/2*((a - 1)^2 + (a + b + c - 3)^2 + (a + 2*b + 4*c - 4)^2 + (a + 3*b + 9*c - 4)^2)
# 도함수(그래디언트)
gradE = E.gradient()

u = vector([1.0, 1.0, 1.0])  # 초기 근사해
tol = 1e-6  # 허용오차 10^(-6)
eta = 0.01  # 학습률(learning rate)

for k in range(5000):
    
    g = gradE(u[0], u[1], u[2])
    gn = g.norm()
              
    if gn <= tol:
        
        print("알고리즘 성공!")
        break
    
    u = u - eta*g

print("u* =", u)
print("E(x*) =", E(u[0], u[1], u[2]))
print("반복 횟수 =", k + 1)

알고리즘 성공!
u* = (1.00000138155249, 2.49999723768073, -0.499999180018564)
E(x*) = 1.59664737265671e-12
반복 횟수 = 4207

즉, 이차함수 𝐲 = a + b𝒙 + c𝒙² 의 계수가 a = 1, b = 2.3, c = -0.5 이므로, 최소제곱곡선은 𝐲 = 1 + 5/2𝒙 - 1/2𝒙² 이다.

✔︎ 도함수의 응용

함수 𝑓가 구간 𝐼에서 정의되어 있을 때, 𝐼 내의 𝒙₁ <𝒙₂인 임의의 두 점 𝒙₁, 𝒙₂에 대하여 𝑓(𝒙₁)<𝑓(𝒙₂)를 만족하면 𝑓는 구간 𝐼에서 증가(increasing)한다고 하며, 𝒙₁ <𝒙₂인 𝐼 내의 임의의 두 점 𝒙₁, 𝒙₂에 대하여 𝑓(𝒙₁)>𝑓(𝒙₂)를 만족하면 𝑓는 구간 𝐼에서 감소(decreasing)한다고 한다. 도함수는 다음과 같이 함수가 증가하거나 감소하는 상황을 알려준다.

함수 𝑓가 폐구간 [a, b]에서 연속이고 개구간 (a, b)에서 미분가능하다고 하자. 그러면 다음이 성립한다.

① 구간 (a, b)내의 모든 점에서 𝑓 '(𝒙) > 0 이면, 𝑓는 [a, b]에서 증가한다.

② 구간 (a, b)내의 모든 점에서 𝑓 '(𝒙) < 0 이면, 𝑓는 [a, b]에서 감소한다.

예를 들어, 𝑓 '(c) > 0 이면 𝒙 = c 에서의 접선의 기울기가 양수이므로, 𝒙 = c 의 근방에서는 함수가 증가함을 알 수 있다.

마찬가지로 𝑓 '(c) < 0 이면 𝒙 = c 의 근방에서는 함수가 감소함을 알 수 있다.

예제 1. 함수 𝑓(𝒙) = 𝒙³-6𝒙²+9𝒙+1이 증가하는 구간과 감소하는 구간을 구하시오.

f(x) = x^3 - 6*x^2 + 9*x + 1
df(x) = diff(f(x), x)
p = plot(f(x), (x, -1, 4), ymin = -5)  # 함수의 그래프
show(p)
print("f'(x) = ", df(x))  # 도함수
solve(df(x) > 0, x)  # 도함수가 0보다 크게 되는 x값의 범위

따라서 함수는 𝒙 < 1, 𝒙 > 3일 때 증가, 1 < 𝒙 < 3 일 때 감소한다.

✔︎ 2계 도함수의 응용

함수 𝑓가 𝒙 = c에서 미분가능하고 (c, 𝑓(c))가 곡선 𝒚 = 𝑓(𝒙) 위의 점이라 할 때, 점 c를 포함하는 적당한 개구간 𝐼가 존재하여 𝒙 ≠ c 인 구간 𝐼의 각 점 𝒙에 대응하는 곡선 위의 모든 점 (𝒙. 𝑓(𝒙))가 점 (c. 𝑓(c))에서의 접선 아래쪽에 있으면 곡선 𝒚 = 𝑓(𝒙)는 점 (c. 𝑓(c))에서 위로 볼록 또는 아래로 오목하다고 하고, 반대로 접선의 위쪽에 있으면 아래로 볼록 또는 위로 오목하다고 한다.

또, 곡선 𝒚 = 𝑓(𝒙)가 점 𝒙 = c에서 연속일 때 (𝑓 '(c))는 존재하지 않아도 무방함), 곡선 위의 점 (c, 𝑓(c))를 경계로 한쪽에서는 위로 볼록하고 다른 쪽에서는 아래로 볼록할 때, (c. 𝑓(c))를 곡선 𝒚 = 𝑓(𝒙)의 변곡점이라 한다. 2계 도함수는 다음과 같이 함수가 위로 볼록하거나 아래로 볼록하는 상황을 알려준다.

함수 𝑓가 점 c를 포함하는 적당한 개구간 𝐼에서 미분가능하고 𝑓 ''(c)가 존재할 때, 다음이 성립한다.

① 𝑓 ''(c) > 0 이면, 곡선 𝑓는 점 (c, 𝑓(c)) 에서 아래로 볼록하다.

② 𝑓 ''(c) < 0 이면, 곡선 𝑓는 점 (c, 𝑓(c)) 에서 위로 볼록하다.

𝑓 ''(c) > 0 이면 𝑓 '' = (𝑓 ')' 이므로 𝑓 ' 는 𝒙 = c 의 근방에서 증가함을 알 수 있고, 𝑓 '은 접선의 기울기를 의미하므로, 접선의 기울기가 증가하는 상황이다. 따라서 다음 그림과 같이 아래로 볼록임을 알 수 있다. 마찬가지로 𝑓 ''(c) < 0 이면 접선의 기울기가 감소하므로 위로 볼록임을 알 수 있다.

예제 2. 함수 𝑓(𝒙) = ⅓𝒙³-𝒙²-3𝒙+4는 어디에서 위로 볼록하고. 아래로 볼록한지 판단하시오.

f(x) = 1/3*x^3 - x^2 - 3*x + 4
df(x) = diff(f(x), x)  # 도함수
d2f(x) = diff(df(x), x)  # 2계 도함수
p = plot(f(x), (x, -3, 5), ymin = -5)  # 함수의 그래프
show(p)
print("f''(x) = ", d2f(x))  # 2계 도함수
solve(d2f(x) > 0, x)  # 2계 도함수가 0보다 큰 x값의 범위
# 1보다 큰 범위에서 함수가 아래로 볼록

따라서 𝒙 < 1 에서 위로 볼록이고, 𝒙 > 1 에서 아래로 볼록이다. (1, ⅓)은 변곡점이다. 

✔︎ 극대, 극소, 최대, 최소

𝑓(𝒙)가 폐구간 [a, b] 에서 연속이면 이 구간에서 𝑓(𝒙)가 최댓값을 취하는 점 및 최솟값을 취하는 점이 존재한다. 함수 𝑓 가 𝒙 = c 의 근방의 모든 점 𝒙에 대하여 𝑓(𝒙) ≤ 𝑓(c) 가 성립하면 함수 𝑓 는 𝒙 = c 에서 극댓값 𝑓(c)를 갖는다. 반대로 함수 𝑓 가 𝒙 = c 의 근방의 모든 점 𝒙에 대하여 𝑓(𝒙) ≥ 𝑓(c) 가 성립하면 함수 𝑓 는 𝒙 = c 에서 극솟값 𝑓(c)를 갖는다. 또, 𝑓 의 극댓값과 극솟값을 통틀어 극값이라 하고, 극대점 또는 극소점 (c, 𝑓(c))를 극점(extreme point)이라 한다.

극값이 생길 수 있는 후보들은 𝑓 '(c) = 0 이거나 𝑓 '(c)가 존재하지 않는 점 𝒙 = c 이다. 함수의 미분계수가 0이거나 존재하지 않는 점을 함수의 임계점(critical point)이라고 한다. 

[Fermat의 임계점 정리]

함수 𝑓 가 개구간 (a, b)에서 연속이고 𝒙 = c(∈(a, b))에서 극값을 갖는다면, 𝑓 '(c) = 0 이거나 𝑓 '(c)가 존재하지 않는다.

예제 3. 함수 𝑓(𝒙) = -2𝒙³+3𝒙²의 임계점을 구하시오.

𝑓 ' = -6𝒙²+6𝒙 = 0에서 임계점은 𝒙 = 0 또는 𝒙 = 1 이다.

f(x) = -2*x^3 + 3*x^2
df(x) = diff(f(x), x)
solve(df(x) == 0, x)

[x == 0, x == 1]

도함수를 이용하면 극댓값과 극솟값을 쉽게 판정할 수 있다. 함수 𝑓 가 정의역 내의 한 점 c 에서 𝑓 '과 𝑓 ''을 가지며, 𝑓 '(c) =0일 때,

① 𝑓 ''(c) < 0이면, 𝑓 (c)는 함수 𝑓 의 극댓값이다.

② 𝑓 ''(c) > 0이면, 𝑓 (c)는 함수 𝑓 의 극솟값이다.

𝑓 ''(c) < 0이면 점 (c, 𝑓(c))에서 위로 볼록인데, 𝑓 '(c) =0 이므로 다음 그림에서 𝑓 (c)는 함수 𝑓 의 극댓값임을 쉽게 알 수 있다. 마찬가지로 𝑓 ''(c) > 0이면 아래로 볼록이므로 𝑓 (c)는 함수 𝑓 의 극솟값임을 알 수 있다.

폐구간에서 연속인 함수 𝑓의 최댓값과 최솟값은 임계점에서의 함숫값과 구간의 양 끝점에서의 함숫값을 비교하여 구하면 된다.

[1 단계] 구간 𝐼 에서 𝑓 의 임계점들을 찾는다.

[2 단계] 이 각각의 임계점들과 양 끝점에서 𝑓 의 값을 계산한다. 그 중 가장 큰 값이 최댓값이고, 가장 작은 값이 최솟값이다.

예제 4. 함수 𝑓(𝒙) = ⅓𝒙³-𝒙²-3𝒙+4가 구간 [-2. 6]에서 정의되었다고 할 때, 𝑓의 극댓값과 극솟값을 구하라.  또, 𝑓의 최댓값과 최솟값을 구하라.

f(x) = 1/3*x^3 - x^2 - 3*x + 4
df(x) = diff(f(x), x)
d2f(x) = diff(df(x), x)
solve(diff(f(x)) == 0, x)  # 여기까지 실행하면 [x == 3, x == -1]을 얻음

print(d2f(3), d2f(-1))  # 3일 때 극댓값, -1일 때 극솟값
print("극댓값 =", f(3))
print("극솟값 =", f(-1))
print(f(-2), f(6))  # 구간의 양 끝점에서의 함숫값과 비교

-4 4
극댓값 = 17/3
극솟값 = -5
10/3 22

따라서 극댓값은 17/3, 극솟값은 -5, 최댓값은 22, 최솟값은 -5 이다.

✔︎ 함수의 극한(limit)

𝒙가 1에 가까이 갈 때 𝑓(𝒙) = (𝒙²-1)/(𝒙-1) 의 값은 어떻게 될까?

함수 𝑓(𝒙) = (𝒙²-1)/(𝒙-1) 은 𝒙 = 1에서 분모가 0이 되므로 함숫값이 정의되지 않는다.

그러나 𝒙 ≠ 1 일 때,

이므로 함수 𝑓(𝒙) 의 그래프는 아래 그림과 같이 𝒙의 값이 1이 아니면서 1에 한없이 가까워질 때, 𝑓(𝒙)의 값은 2에 한없이 가까워짐을 알 수 있다.

즉, 

f(x) = (x^2 - 1)/(x - 1)  # 함수 정의
n = 10
for i in range(1, n):   # 1보다 크면서 1에 가까이 있는 x값에 대해서 f(x)계산
    s = (1 + 1/(10^i)).n()
    print("x =", s, "f(x) =", f(s).n()) 
print()  # 한 줄 비우기
for i in range(1, n):   # 1보다 작으면서 1에 가까이 있는 x값에 대해서 f(x)계산
    s = (1 - 1/(10^(n - i))).n()
    print("x =", s, "f(x) =", f(s).n())

plot(f(x), (x, 0, 2))

limit((x^2 - 1)/(x - 1), x = 1)  # limit(f(x), x = a)

2

따라서 함수 𝑓(𝒙) = (𝒙²-1)/(𝒙-1) 은 𝒙의 값이 1이 아니면서 1에 한없이 가까이 갈 때, 2에 한없이 가까워진다. 이를

와 같이 나타낸다. 

이처럼 𝒙가 a에 가까이 갈 때 𝑓(𝒙)는 b에 가까워지면, "𝒙→a 일 때 𝑓(𝒙)는 b에 수렴한다"고 하고

로 표기한다. 이때 b를 𝑓(𝒙)의 극한(limit)이라고 부른다. 수렴하지 않으면 발산한다고 한다.

* 함수의 극한에서는 𝒙 = a 일 때 𝑓(𝒙) 값의 존재여부가 중요하지 않다. 즉, 𝑓(𝒙)가 존재하지 않아도 극한은 정의될 수 있다(ex. 발산). 만일 𝑓(a)가 정의되고 

이면 𝑓(𝒙)는 𝒙 = a에서 연속(continuous)이라고 한다.

예제 2. 다음의 극한을 구하시오.

g(x) = sin(x)/(x + 1)
show(g(x))
show(plot(g(x), (x, -2, 4), ymin = -5, ymax = 5, detect_poles = 'show'))
print(limit(g(x), x = 2))  # x = 2일 때 극한
print()

f(x) = (x^2 - 4)/abs(x - 2)
show(f(x))
show(plot(f(x), (x, -2, 4), ymin = -5, ymax = 5, detect_poles = 'show'))
print(limit(f(x), x = 2, dir = '-'))  # x = 2일 때 좌극한
print(limit(f(x), x = 2, dir = '+'))  # x = 2일 때 우극한

↔︎ 우극한과 좌극한이 모두 존재하고, 그 값이 같으면 그 지점에서의 극한값이 존재한다고 한다. 

✔︎ 도함수(derivative)와 미분(differentiation)

점 P(1, 1)에서 포물선 𝒚 = 𝒙² 에 대한 접선의 방정식을 구하시오.

함수 𝑓(𝒙) 위의 점 P(𝒙₀, 𝑓(𝒙₀)) 에서 접선의 기울기가 𝑚 임을 알면 다음 공식에 의해 접선의 방정식을 쉽게 구할 수 있다.

𝒚 - 𝑓(𝒙₀) = 𝑚(𝒙-𝒙₀)

우선, 포물선 𝒚 = 𝒙² 위의 점 P(1, 1) 근처에서 한 점 Q(𝒙, 𝒙²)를 선택하여 할선 PQ의 기울기를 구하자.

이제 점 Q를 점 P로 이동함에 따라 할선 PQ는 접선에 가까워짐을 볼 수 있다. 따라서 접선의 기울기는 할선 PQ의 기울기의 Q→P일 때의 극한으로 정의하는 것이 타당하다.

포물선 𝒚 = 𝒙² 위의 점 P(1, 1) 에서의 접선의 방정식은 다음과 같다.

𝒚 - 1 = 2(𝒙 - 1) 즉, 𝒚 = 2𝒙 - 1 

함수 𝑓의 정의역 내에 속하는 점 a에 대하여, 극한값

이 존재하면 함수 𝑓는 𝒙 = a에서 미분가능(differentiable)하다고 하고, 이 극한값을 𝒙 = a에서의 함수 𝑓의 미분계수(differential coefficient)라 하며 𝑓 '(a)로 나타낸다. 앞서 언급한 접선을 생각하면 미분계수는 접선의 기울기를 나타낸다. 따라서 (𝒙₀, 𝑓(𝒙₀))에서의 접선의 방정식은 다음과 같이 쓸 수 있다.

𝒚 - 𝑓(𝒙₀) = 𝑓 '(𝒙₀)(𝒙 - 𝒙₀)

𝑓(𝒙)는 𝒙 = a 에서 미분가능이면 𝒙 = a 에서 연속이다 (그러나 역은 성립하지 않는다). 즉 𝑓(𝒙)가 𝒙 = a 에서 연속이라도 반드시 미분가능인 것은 아니다.

𝒚 = 𝑓(𝒙)가 어떤 구간의 각 점 𝒙에서 미분가능일 때 𝑓(𝒙)는 이 구간에서 미분가능이라고 한다.

이 경우 각 점 𝒙에 그 점에서의 미분계수를 대응시킴으로써 정해지는 함수를 𝑓(𝒙)의 도함수(derivative)라 하고 다음 기호들로 나타낸다.

함수 𝑓(𝒙)의 도함수를 구하는 것을 𝑓(𝒙)를 미분한다(differentiate)고 하고, 함수 𝒚 = 𝑓(𝒙)의 도함수는 식

으로 구한다. 따라서 어떤 함수를 미분하여 얻은 그 함수가 도함수이고, 거기에 변수의 값을 대입하면 그 점에서의 미분계수가 나오는 것이다.

함수 𝒚 = 𝑓(𝒙)의 도함수 𝒚' = 𝑓 '(𝒙)가 다시 미분가능이면 그 도함수 (𝒚')'를 𝒚 = 𝑓(𝒙)의 2계 도함수(2nd derivative)라 하고, 

등으로 나타낸다. 2계 도함수가 또 다시 미분가능이면 3계 도함수(3rd derivative)를 생각할 수 있게 된다. 이와 같이 𝒚 = 𝑓(𝒙)를 계속하여 n번 미분하면 n계 도함수가 정의되며, n계 도함수(n-th derivative)는 다음 기호로 나타낸다.

𝑓⁽ⁿ⁾(𝒙)가 존재하는 경우 𝑓(𝒙)는 n번 미분가능하다고 한다. 미분계수의 응용인 속도와 가속도는 각각 거리를 나타내는 함수의 1계 도함수와 2계 도함수의 예이다.

* 미분에 관하여 다음이 성립한다.

예제 2. 𝒚 = 𝒙² + 4𝒆ˣ의 도함수와 2계 도함수 𝒚'', 3계 도함수 𝒚'''를 구하시오.

f(x) = x^2 + 4*e^x
print(diff(f(x), x))   # dy/dx
print(diff(f(x), x, 2))  # 2계도함수
print(diff(f(x), x, 3))  # 3계도함수

2*x + 4*e^x
4*e^x + 2
4*e^x

식이 복잡해지면 미분가능한지에 대한 여부만 판단한 후 코드로 도함수를 구한다.

예제 3. 𝒚 = 𝒙² + √𝒙 위의 점 (4, 18)에서의 접선의 방정식을 구하시오.

풀이)

f(x) = x^2 + sqrt(x)
x0 = 4
df(x) = diff(f(x), x)    # 도함수 구하기
print("접선의 방정식 :  y =", f(x0) + df(x0)*(x - x0))
p1 = plot(f(x), (x, 0, 10))   # 함수 f(x) 그리기
p2 = plot(f(x0) + df(x0)*(x - x0), (x, 0, 10), color = 'red')   # 접선 그리기
p1 + p2   # 함수 f(x)와 접선을 동시에 보여주기

최소제곱법은 데이터들의 패턴과 분포(behavior)를 잘 표현하는 근사직선이나 근사곡선을 구하는 아주 직관적이며 간단한 방법으로, 수치해석. 회귀분석. 영상처리. 로봇 위치상태 분석 분야에서도 다양하게 활용된다.

✔︎ 최소제곱문제

다음과 같이 𝒙와 𝒚에 관한 2차원 데이터가 주어져 있다고 하자.

이를 좌표평면에 나타내면 아래의 왼쪽 그림과 같다. 우리는 직관적으로 𝒙와 𝒚의 관계를 아래 오른쪽 그림과 같이 직선(파란색 점선)으로 나타낼 수 있음을 알 수 있다. 이를 최소제곱직선이라 한다.

이제 최소제곱직선을 찾아보자. 즉, 𝒙와 𝒚의 관계를 가장 잘 보여주는 일차함수 𝒚 = a𝒙 + b를 찾는다. 가장 이상적인 상황은 모든 데이터 (𝒙, 𝒚𝒾)에 대해서 𝒚𝒾 = a𝒙𝒾 + b가 만족되는 𝒚𝒾절편 a와 기울기 b를 찾는 것이다. 따라서 다음과 같이 미지수가 a, b인 선형연립방정식과 행렬표현을 얻게 된다.

직선을 구하기 위해서는 (즉 a와 b를 찾기 위해서는) 두 개의 데이터(두 점)에 대한 정보만 있으면 충분하다. 그러나 측정에서 생기는 오차의 영향을 줄이기 위하여 대개는 미지수의 개수보다 많은 개수의 데이터를 사용하므로 방정식의 수가 미지수의 개수보다 많은 선형연립방정식이 생긴다. 이런 경우, 일반적으로 선형연립방정식을 만족하는 해(즉 Au = y인 u)를 기대할 수 없다.

대신 Au와 y 사이의 거리(dist(Au, y) = ||Au-y||)가 최소가 되는 근사해, 즉 다음을 만족하는 û을 찾는 문제를 최소제곱문제(least square problem)라 한다.         

여기서 min은 '최소화 한다'는 의미이고 û은 Au=y의 최소제곱해(least square solution)이다.

✔︎ 최소제곱문제의 의미

각 데이터 (𝒙𝒾, 𝒚𝒾)에 대하여 𝒙𝒾를 일차함수 𝒚=a+b𝒙에 대입하여 얻은 값을 ŷ𝒾라 하자(즉 ŷ𝒾=a+b𝒙𝒾). [표 1]의 선형연립방정식의 해가 존재하지 않는 경우는 각 데이터에 따라서 𝒚𝒾와 ŷ𝒾가 같지 않아서 발생하므로, 이를 해결하기 위한 차선책으로 각 데이터의 (제곱)오차 (𝒚𝒾-ŷ𝒾)²가 최소가 되는 a, b를 구한다. 주어진 모든 데이터에 대한 오차(error)를 더하면 다음을 얻는다. 

따라서 최소제곱문제는 아래와 같이 오차를 최소화하는 (최적화, optimization)문제로 이해할 수 있다.

✔︎ 정사영과 최소제곱해

먼저 다음 식을 만족하는 해 𝑡를 찾는 문제를 보자.

이 문제는 시작점이 같은 두 벡터 a와 x에 대하여 a를 포함하는 직선과 x사이의 거리가 최소가 되게 하는 𝑡를 찾으려고 하는 것이다.

ta는 a와 평행이므로 a를 포함하는 직선위에 놓이게 되고 [그림 2]에서 보듯이 실수 t의 값에 대하여 ||ta-x||는 실선으로 표시된 선분의 길이를 나타낸다. 직관적으로 ta 중 x와의 거리가 가장 짧은 벡터는 x의 끝점에서 a를 포함하는 직선 위에 수선을 내려 생기는 벡터 p(=ta)임을 쉽게 알 수 있다. 그리고 이때의 t값이 min||ta-x||의 해가 된다. 벡터 p를 a 위로의 x의 정사영(projection)이라고 한다. 실수 t를 구하기 위해 (x-ta)⊥a임을 이용하면 다음을 얻는다.

✔︎ 데이터에 적합한 곡선 찾기(Curve Fitting)

앞서 학습한 방법을 활용하여 𝒙와 𝒚의 관계를 가장 잘 보여주는(best fit 하는) 이차식 (근사식) 𝒚=a+b𝒙+c𝒙²도 찾을 수 있다. 

즉 다음과 같이 미지수가 a, b, c인 선형연립방정식과 행렬표현을 얻게 된다.

방정식의 수가 미지수의 개수보다 많은 선형연립방정식이 생기면 다음과 같은 최소제곱문제가 발생하고,

이를 오차로 표현하면 다음과 같다.

같은 방법으로 행렬을 이용하여 다음과 같이 구할 수 있다.

✔︎ 첨가행렬(augmented matrix)

선형연립방정식은 행렬을 이용하여 표현할 수 있다. 다음과 같이 𝑛개의 미지수를 갖는 𝑚개의 선형방정식에 대하여

벡터를 이용하여 표기하면 다음과 같다. 

이를 행렬의 곱을 이용하여 표현하면 

가 된다. 

라 놓으면 선형연립방정식은 다음과 같이 간단히 쓸 수 있다.

이때 행렬 A를 선형연립방정식의 계수행렬(coefficient matrix)이라 하며, A에 b를 붙여서 만든 행렬

을 선형연립방정식의 첨가행렬이라고 한다.

예제 1. 다음 선형연립방정식의 첨가행렬을 구하시오.

A = matrix([[1, 1, 2], [2, 4, -3], [3, 6, -5]])  # 계수행렬 입력
b = vector([9, 1, 0])  # 상수항 벡터
print("[A : b] =")
A.augment(b)  # 첨가행렬

[A : b] =
[ 1  1  2  9]
[ 2 4 -3  1]
[ 3 6 -5 0]

* 𝑛차의 정사각행렬 A가 가역이고 b가 ℝ^𝑛의 벡터일 때, 연립방정식 Ax=b는 유일한 해 x = A^(-1)b를 갖는다.

예제 2. 역행렬을 이용하여 다음 연립방정식 Ax = b의 해를 구하시오.

A = matrix(3, 3, [1, 2, 3, 2, 5, 3, 1, 0, 8]) 
b = vector([1, 3, -1])
print("x =", A.inverse()*b)  # 역행렬을 이용한 연립방정식의 해 구하기
print()
print("x =", A.solve_right(b))  # .solve_right( )를 이용하여 구할 수도 있다.

x = (-1, 1, 0)
x = (-1, 1, 0)

✔︎ 가우스 소거법

- 가우스 소거법은 위의 예시에서와 같이 첨가행렬을 간단하게 하는 것.

- 즉, 기본행 연산을 사용하여 첨가행렬을 왼쪽에서 오른쪽의 형태로 바꾸어 계산하는 것.

- 오른쪽의 형태를 기약 행 사다리꼴(reduced row echelon form, RREF)이라고 한다.

• 성분이 모두 0인 행이 존재하면 그 행은 행렬의 맨 아래에 위치한다.
• 각 행에서 처음으로 나타나는 0이 아닌 성분은 1이다. 이때 이 1을 그 행의 선행성분(leading entry, leading 1)이라고 한다.
• i행과 (i+1)행 모두에 선행성분이 존재하면 (i+1)행의 선행성분은 i행의 선행성분보다 오른쪽에 위치한다.
• 선행성분(leading entry in row)을 포함하는 열의 선행성분 외의 성분은 모두 0이다.

예제 3. 다음 선형연립방정식의 해를 계산하고, 직접 계산한 결과와 코딩 프로그램을 이용하여 계산한 결과를 비교하시오. (해가 유일한 경우)

A = matrix([[2, -3, 1], [7, 1, -2], [1, 4, 3]])  # 계수행렬
b = vector([10, 1, -9])  # 상수항 벡터
A.augment(b).rref()  # 첨가행렬의 RREF

[ 1 0 0 39/59]
[ 0 1 0 -162/59]
[ 0 0 1 26/59]

결과)

Sage의 내부 명령어로부터 구할 수도 있다.

A = matrix([[2, -3, 1], [7, 1, -2], [1, 4, 3]])  # 계수행렬
b = vector([10, 1, -9])  # 상수항 벡터
A.solve_right(b)

(39/59, -162/59, 26/59)

✔︎ 연립방정식의 해집합

예제 4. 다음 연립방정식의 해를 계산하시오. (해가 무수히 많은 경우)

A = matrix([[3, -2, 1, -1, 5], [2, 1, -2, 3, 0], [1, 5, 4, -7, 1]])
b = vector([1, 23, -17])
A.augment(b).rref()

[ 1 0 0 4/71 73/71 262/71]
[ 0 1 0 -13/71 -42/71 107/71]
[ 0 0 1 -109/71 52/71 -501/71]

위의 결과가 의미하는 것은

     즉,   

이다. 따라서 𝒖와 𝒗의 값이 정해지면 그에 따라 𝒙, 𝒚, 𝒛의 값이 정해진다. 𝒖 = 𝒓. 𝒗 = 𝒔(𝒓. 𝒔는 임의의 실수)를 대입하면 다음을 얻는다.

이 해를 벡터 형태로 쓰면 다음과 같다.

𝒓과 𝒔에 임의의 실수를 대입하여 얻은 (𝒙, 𝒚, 𝒛, 𝒖, 𝒗)는 모두 해가 된다. 따라서 무수히 많은 해를 갖는다.

(이때 𝒓과 𝒔를 자유변수(free variable)이라고 한다.)

Sage의 내부 명령어가 주는 해는 위의 일반해 중 𝒓 = 0, 𝒔 = 0인 경우의 특수해(Special solution)만 제공한다.

A = matrix([[3, -2, 1, -1, 5], [2, 1, -2, 3, 0], [1, 5, 4, -7, 1]])
b = vector([1, 23, -17])
A.solve_right(b)

(262/71, 107/71, -501/71, 0, 0)

예제 5. 다음 연립방정식의 해를 계산하시오. (해가 없는 경우)

A = matrix([[1, -2, 1], [2, -2, 1], [3, 1, -5], [0, -1, 2], [-6, 0, 7]])
b = vector([7, 5, 0, -4, -10])
A.augment(b).rref()

[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
[0 0 0 0]

위의 결과가 의미하는 것은

이다. 따라서 네 번째 식 0 = 1 이 모순이므로 이 연립방정식은 해가 존재하지 않는다. 

(Sage의 내부 명령어를 이용하면 ValueError 발생)

🔑 정리하기

데이터의 특징에 따라 데이터가 어느 범주에 속하는지 판단하는 것을 우리는 분류(classification)하고 한다. 이를 위해서는 데이터 들이 서로 얼마나 가까운지 즉 유사한지를 판단할 수 있어야 하는데, 먼저 거리를 이용하여 데이터가 얼마나 유사한지 판단하는 거리 척도와 그를 위한 벡터의 노름(norm)에 대하여 학습한다. 그리고 데이터의 패턴, 방향에만 관심이 있는 경우 사용할 수 있는 척도인 코사인 유사도와 내적(inner product)에 관하여 학습한다.

✔︎ 데이터의 유사도

- 분류(classification): 주어진 데이터의 특징에 따라 데이터가 어느 범주(class 또는 category)에 속하는지 판단하는 것.

- 유사도(similarity): 분류를 위한 데이터의 척도. 주어진 데이터를 분류하기 위해서는 각 데이터마다 우리가 다룰 수 있는 (계산할 수 있는) 형태로 표현할 수 있고, 각 범주와 얼마나 가까운지 (혹은 유사한지) 계산하여 최종 판단해야 한다. 

✔︎ 거리

- 유사도는 가장 쉽게 거리로 측정 가능. 데이터는 순서쌍(pair), 순서조(n-tuple) 또는 벡터(vector)로 표현할 수 있다.

- 예를 들어, 두 점 A(a1, a2), B(b1, b2) 사이의 거리는 다음과 같이 계산한다. (유클리드 거리)

- 거리가 가까우면 두 데이터는 유사하다고 볼 수 있고, 거리가 멀면 두 데이터는 관계없다고 판단할 수 있다.

✔︎ 노름(norm, 크기)

- 벡터 a = (a1, a2)에 대하여 a의 크기를 다음과 같이 나타내고, a의 노름(norm)이라 한다.

- ||a||는 원점에서 점 A(a1, a2)에 이르는 거리와 같다. 두 벡터 a = (a1, a2), b = (b1, b2)에 대하여 ||a-b||는 두 점 A(a1, a2), B(b1, b2) 사이의 거리(distance)가 되며, 다음이 성립한다.

- 위 정의는 3차원은 물론 고차원 데이터에 대해서도 동일한 형태로 확장된다. 예를 들어, 3차원 데이터 a = (a1, a2, a3), b = (b1, b2, b3)에 대하여 A(a1, a2, a3), B(b1, b2, b3)라 할때 다음이 성립한다.

✔︎ 노름(크기, 거리)을 활용한 데이터의 유사도 비교

예제: 세 개의 데이터 A(0, 1, -7, 1), B(5, 2, -1, 3), C(-2, 0, -4, 6)에 대하여 B는 A와 C 중 어느 데이터에 더 가까운지 판단하시오.

a = vector([0, 1, -7, 1])  # 벡터 생성
b = vector([5, 2, -1, 3])
c = vector([-2, 0, -4, 6])
distAB = (a - b).norm()  # dist(A, B)
distBC = (b - c).norm()  # dist(B, C)
print("dist(A, B) =", distAB)
print("dist(B, C) =", distBC)
bool(distAB < distBC)  # True 이면 dist(A, B) < dist(B, C) 성립

dist(A, B) = sqrt(66)
dist(B, C) = sqrt(71)
True

✔︎ 사잇각을 활용한 데이터의 비교

- 데이터 분석가가 단지 데이터의 패턴(방향)에만 관심이 있는 경우, (거리)척도는 적합하지 않다.

- 예를 들어, 아래와 같이 좌표평면 상에 벡터로 표현된 두 데이터 a = (a1, a2)와 b = (b1, b2)는 패턴(방향)은 유사하지만 거리는 매우 큰 값을 갖게 되어, (거리)척도로는 “두 데이터가 관계가 없다”고 판단하게 되기 때문이다.

✔︎ 코사인 유사도의 개념

- 단지 데이터의 패턴(방향)에만 관심이 있는 경우에는 유사도는 두 데이터(벡터)가 이루는 사잇각𝞱으로 측정 가능.

- 𝞱가 작으면 데이터의 유사도가 높고, 𝞱가 크면 데이터의 유사도가 낮다.

- 벡터의 내적을 이용하여 𝞱의 코사인 값으로 유사도를 측정.

✔︎ 내적

- 두 벡터 a = (a1, a2), b = (b1, b2)의 내적(inner product)은 다음과 같이 정의된다.

- 내적은 다음의 성질을 만족하는데, 대부분은 실수의 곱셈이 만족하는 성질과 유사하다.

✔︎ 사잇각                 

이 식을 벡터를 이용하여 다시 표현하면 다음과 같다. 

또한 내적의 정의와 성질에 의해 

이므로, 위의 두 식을 비교하면 다음을 얻는다. 

두 벡터가 주어지면 언제나 이 식을 만족하는 θ가 존재하게 되고, 그 θ가 두 벡터 a와 b의 사잇각(angle)이다.

✔︎ 코사인 유사도 계산

두 데이터 a = (a1, a2), b = (b1, b2)의 코사인 유사도는 다음과 같이 계산할 수 있다. 𝓷차원 공간 ℝ^𝓷의 두 벡터 a = (a1, a2, a3, ..., an), b = (b1, b2, b3, ..., bn)에 대해서도 동일한 공식이 성립.

는 원데이터 a, b의 크기에 관계없이 크기가 항상 1인 단위벡터(unit vector)이므로

코사인 유사도는 데이터의 크기와 데이터 사이의 거리는 무시하고 단지 데이터의 패턴(방향)만 고려하게 된다. 코사인 함수의 성질에 의해 코사인 값이 크면  사잇각은 작아지게 되고, 그에 따라 유사도는 높아지게 된다. 이런 방식으로 데이터 사이의 패턴을 분석할 수 있다.

예제: 두 벡터 v = (1, 2, -4) 와 w = (-1, 3, 1)에 대하여 내적 v•w, 코사인 유사도, 그리고 사잇각 𝞱(0≤𝞱≤𝛑)를 계산하시오.

v = vector([1, 2, -4])  # 벡터 생성
w = vector([-1, 3, 1])
vw = v.inner_product(w)  # 두 벡터의 내적. 형식은 a.inner_product(b)
vn = v.norm()
wn = w.norm()
cos_sim = vw/(vn*wn)  # 코사인 유사도
ang = arccos(cos_sim)  # 사잇각(라디안)
print("v.w =", vw)
print("||v|| =", vn)
print("||w|| =", wn)
print("cos_similarity =", cos_sim.n(digits = 3))
print("angle(rad) =", ang.n(digits = 3))
# .n(digits = d)는 유효숫자 d자리의 근삿값

v.w = 1
||v|| = sqrt(21)
||w|| = sqrt(11)
cos_similarity = 0.0658
angle(rad) = 1.51

예제: 코사인 유사도를 활용하여 세 개의 데이터 A(0, 1, -7, 1), B(5, 2, 1, 3), C(-2, 0 -4, 6)에 대하여 B는 A와 C 중 어느 데이터에 더 가까운지 판단하시오.

a = vector([0, 1, -7, 1])  # 벡터 생성
b = vector([5, 2, 1, 3])
c = vector([-2, 0, -4, 6])
cos_simAB = a.inner_product(b)/(a.norm()*b.norm())  # 코사인 유사도
cos_simBC = b.inner_product(c)/(b.norm()*c.norm())
print("cos_sim(A, B) =", cos_simAB.n(digits = 3))
print("cos_sim(B, C) =", cos_simBC.n(digits = 3))
bool(cos_simAB < cos_simBC)

cos_sim(A, B) = -0.0448
cos_sim(B, C) = 0.0856
True

🔑 정리하기

- 데이터를 분류할 때 데이터끼리 얼마나 유사한지를 판단하는 방법은 두 가지가 있다: 거리와 방향

- 거리는 노름(norm)으로 구하고, 방향은 사잇각𝞱으로 구한다.

- 사잇각을 구하기 위해 필요한 개념은 내적(inner product)과 코사인 유사도(similarity)이다.

- 두 벡터 a = (a1, a2), b = (b1, b2)의 내적

- 피타고라스의 정리와 내적의 성질로 구한 코사인 유사도

(0≤𝞱≤𝛑)

- 코사인 함수의 성질에 의해 코사인 값이 크면 사잇각은 작아지게 되고, vice versa.

- '𝞱 = arccos(cos𝞱)' 이 코드로 사잇각 계산

✔︎ 순서쌍과 벡터(Vector)

데이터는 순서쌍(ordered pair, tuple)으로 표현할 수 있다. 예를 들어, 어떤 사람의 키, 몸무게, 연령, 성별 등은 그 사람에 관한 데이터가 될 수 있고, 이는 다음과 같이 순서쌍으로 나타낼 수 있다. 여기서 키, 몸무게, 연령, 성별 각각은 데이터를 이루는 성분이다.

특히 성분이 2개(3개)로 이루어진 2차원(3차원) 데이터는 좌표평면(좌표공간)상의 한 점을 나타낸다. 마찬가지로 4차원 이상의 데이터는 우리 눈으로 볼 수 있도록 시각화 할 수 없지만, 고차원 공간 상에 놓인 점이라고 볼 수 있다. 예를 들어, 아래에서 a1, a2를 성분으로 하는 데이터 (a1, a2)는 좌표평면 상의 한 점 A를 나타낸다. 이때 시작점을 원점 O, 끝점을 A로 하는 화살표로 나타낸 것을 벡터(vector)라 하고 

로 표기한다. 그리고 벡터를 이루는 각각의 성분은 하나의 숫자로 이루어져 있는데 이를 스칼라(scalar)라고 한다.

✔︎ 행렬(Matrix)과 텐서(Tensor)

앞서 언급한 어떤 사람의 키, 몸무게, 연령, 성별에 대한 데이터를 하나로 모아 다음과 같이 직사각형 모양으로 배열할 수 있다. 이를 행렬(matrix)이라 한다. 즉, 행렬은 벡터를 여러 개 쌓아서 만든 것으로 이해해도 된다. 이때 가로를 행(row), 세로를 열(column)이라 하고, 행의 개수가 m, 열의 개수가 n인 행렬을 크기가 mxn인 행렬이라고 한다. 따라서 벡터는 1xn 행렬(행벡터) 또는 nx1 행렬(열벡터)로 이해할 수 있다.

또한 행렬은 디지털 이미지를 유용하게 나타낼 수 있다. 예를 들어, 디지털 이미지를 확대할 때 나타나는 작은 격자를 픽셀(pixel, 화소)이라 하는데, 각 픽셀에는 이미지의 밝은 정도를 나타내는 숫자가 들어 있다고 볼 수 있다. 그리고 흑백 이미지는 하나의 행렬로 나타낼 수 있고, 컬러 이미지는 빨강(Red), 녹색(Green), 파랑(Blue), 3개의 채널(channel)로 표현되어 행렬이 3차원으로 겹쳐진 Cube 형태의 모양을 갖는다. 이를 3-D 텐서(tensor)라 한다.

텐서는 데이터를 한군데 모아 놓을 수 있는 저장소인 컨테이너(container)이다. 1-D 텐서가 벡터이고, 2-D 텐서가 행렬이다. 즉, 행렬의 일반화된 모습을 텐서라고 생각할 수 있다.

✔︎ 행렬 연산 - 곱셈

✔︎ 행렬의 연산 법칙

(1) 전치행렬(transpose matrix) : 행렬 A의 행과 열을 바꾸어 얻어진 행렬을 Aᵀ로 나타낸다. A가 2x3 행렬이면 Aᵀ는 3x2 행렬이 된다.

(2) 대각선 행렬(diagonal matrix) :  주대각선성분 이외의 모든 성분이 0인 정사각행렬. 

(3) 단위행렬(identity matrix): 주대각선성분이 모두 1인 대각선 행렬.

- 단위행렬은 행렬의 곱셈에 대한 항등원 역할을 한다. 

(3) 삼각행렬

- 하삼각행렬(lower triangular matrix): 주대각선 위의 모든 성분이 0인 정사각행렬

- 상삼각행렬(upper triangular matrix)은 주대각선 아래의 모든 성분이 0인 정사각행렬

(4) 대칭행렬(symmetric matrix) : Aᵀ = A를 만족하는 정사각행렬

(5) 역행렬(inverse matrix) :  n×n의 정사각행렬 A에 대하여 다음을 만족하는 행렬 B가 존재하면 A는 가역(invertible, nonsingular).     

이때 B를 A의 역행렬(inverse matrix)이라고 하며, A⁻¹로 나타낸다. 이러한 B가 존재하지 않으면 A는 비가역(noninvertible) 또는 특이행렬(singular matrix)이라고 한다. n차의 정사각행렬 A, B가 가역이고 k가 0이 아닌 스칼라일 때, 다음이 성립한다.