✔︎ 첨가행렬(augmented matrix)
선형연립방정식은 행렬을 이용하여 표현할 수 있다. 다음과 같이 𝑛개의 미지수를 갖는 𝑚개의 선형방정식에 대하여
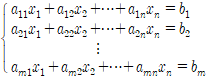
벡터를 이용하여 표기하면 다음과 같다.
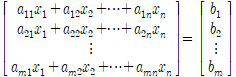
이를 행렬의 곱을 이용하여 표현하면

가 된다.

라 놓으면 선형연립방정식은 다음과 같이 간단히 쓸 수 있다.
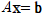
이때 행렬 A를 선형연립방정식의 계수행렬(coefficient matrix)이라 하며, A에 b를 붙여서 만든 행렬
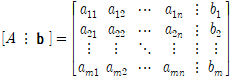
을 선형연립방정식의 첨가행렬이라고 한다.
예제 1. 다음 선형연립방정식의 첨가행렬을 구하시오.
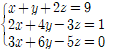
A = matrix([[1, 1, 2], [2, 4, -3], [3, 6, -5]]) # 계수행렬 입력
b = vector([9, 1, 0]) # 상수항 벡터
print("[A : b] =")
A.augment(b) # 첨가행렬[A : b] =
[ 1 1 2 9]
[ 2 4 -3 1]
[ 3 6 -5 0]
* 𝑛차의 정사각행렬 A가 가역이고 b가 ℝ^𝑛의 벡터일 때, 연립방정식 Ax=b는 유일한 해 x = A^(-1)b를 갖는다.
예제 2. 역행렬을 이용하여 다음 연립방정식 Ax = b의 해를 구하시오.
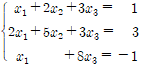
A = matrix(3, 3, [1, 2, 3, 2, 5, 3, 1, 0, 8])
b = vector([1, 3, -1])
print("x =", A.inverse()*b) # 역행렬을 이용한 연립방정식의 해 구하기
print()
print("x =", A.solve_right(b)) # .solve_right( )를 이용하여 구할 수도 있다.x = (-1, 1, 0)
x = (-1, 1, 0)
✔︎ 가우스 소거법

- 가우스 소거법은 위의 예시에서와 같이 첨가행렬을 간단하게 하는 것.
- 즉, 기본행 연산을 사용하여 첨가행렬을 왼쪽에서 오른쪽의 형태로 바꾸어 계산하는 것.

- 오른쪽의 형태를 기약 행 사다리꼴(reduced row echelon form, RREF)이라고 한다.
- 성분이 모두 0인 행이 존재하면 그 행은 행렬의 맨 아래에 위치한다.
- 각 행에서 처음으로 나타나는 0이 아닌 성분은 1이다. 이때 이 1을 그 행의 선행성분(leading entry, leading 1)이라고 한다.
- i행과 (i+1)행 모두에 선행성분이 존재하면 (i+1)행의 선행성분은 i행의 선행성분보다 오른쪽에 위치한다.
- 선행성분(leading entry in row)을 포함하는 열의 선행성분 외의 성분은 모두 0이다.

예제 3. 다음 선형연립방정식의 해를 계산하고, 직접 계산한 결과와 코딩 프로그램을 이용하여 계산한 결과를 비교하시오. (해가 유일한 경우)
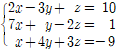
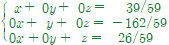
A = matrix([[2, -3, 1], [7, 1, -2], [1, 4, 3]]) # 계수행렬
b = vector([10, 1, -9]) # 상수항 벡터
A.augment(b).rref() # 첨가행렬의 RREF[ 1 0 0 39/59]
[ 0 1 0 -162/59]
[ 0 0 1 26/59]
결과)
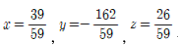
Sage의 내부 명령어로부터 구할 수도 있다.
A = matrix([[2, -3, 1], [7, 1, -2], [1, 4, 3]]) # 계수행렬
b = vector([10, 1, -9]) # 상수항 벡터
A.solve_right(b)(39/59, -162/59, 26/59)
✔︎ 연립방정식의 해집합
예제 4. 다음 연립방정식의 해를 계산하시오. (해가 무수히 많은 경우)
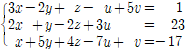
A = matrix([[3, -2, 1, -1, 5], [2, 1, -2, 3, 0], [1, 5, 4, -7, 1]])
b = vector([1, 23, -17])
A.augment(b).rref()[ 1 0 0 4/71 73/71 262/71]
[ 0 1 0 -13/71 -42/71 107/71]
[ 0 0 1 -109/71 52/71 -501/71]
위의 결과가 의미하는 것은
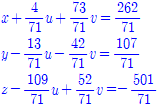
즉,
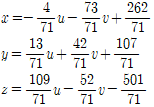
이다. 따라서 𝒖와 𝒗의 값이 정해지면 그에 따라 𝒙, 𝒚, 𝒛의 값이 정해진다. 𝒖 = 𝒓. 𝒗 = 𝒔(𝒓. 𝒔는 임의의 실수)를 대입하면 다음을 얻는다.
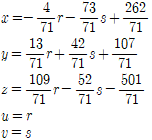
이 해를 벡터 형태로 쓰면 다음과 같다.
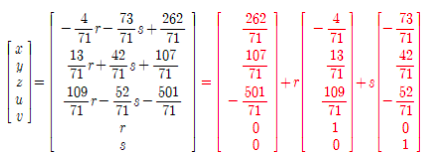
𝒓과 𝒔에 임의의 실수를 대입하여 얻은 (𝒙, 𝒚, 𝒛, 𝒖, 𝒗)는 모두 해가 된다. 따라서 무수히 많은 해를 갖는다.
(이때 𝒓과 𝒔를 자유변수(free variable)이라고 한다.)
Sage의 내부 명령어가 주는 해는 위의 일반해 중 𝒓 = 0, 𝒔 = 0인 경우의 특수해(Special solution)만 제공한다.
A = matrix([[3, -2, 1, -1, 5], [2, 1, -2, 3, 0], [1, 5, 4, -7, 1]])
b = vector([1, 23, -17])
A.solve_right(b)(262/71, 107/71, -501/71, 0, 0)
예제 5. 다음 연립방정식의 해를 계산하시오. (해가 없는 경우)

A = matrix([[1, -2, 1], [2, -2, 1], [3, 1, -5], [0, -1, 2], [-6, 0, 7]])
b = vector([7, 5, 0, -4, -10])
A.augment(b).rref()[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
[0 0 0 0]
위의 결과가 의미하는 것은
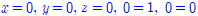
이다. 따라서 네 번째 식 0 = 1 이 모순이므로 이 연립방정식은 해가 존재하지 않는다.
(Sage의 내부 명령어를 이용하면 ValueError 발생)
🔑 정리하기

'◦ Machine Learning > Mathmatics' 카테고리의 다른 글
| [기초수학] 극대, 극소, 최대, 최소 (0) | 2021.01.11 |
|---|---|
| [기초수학] 극한과 도함수 (0) | 2021.01.11 |
| [기초수학] 정사영과 최소제곱문제 (0) | 2021.01.09 |
| [기초수학] 데이터이 분류 (0) | 2021.01.08 |
| [기초수학] 데이터와 행렬 (0) | 2021.01.07 |