✔︎ 경사하강법(Gradient Descent Algorithm)
경사하강법은 함수 𝑓 가 복잡하여 방정식을 풀어서 임계점을 구하는 것이 힘들 때 사용한다. 경사하강법의 기본 아이디어는 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜서 극값에 이를 때까지 반복시키는 것이다.
[알고리즘]

[작동 원리]
우선 임의로 𝒙₁ 을 정하여 𝒈₁ = 𝑓 '(𝒙₁) 을 계산한다. 만일 |𝒈₁| ≤ ɛ (여기서 ɛ는 예를 들어, ɛ = 10⁻⁶ 과 같이 매우 작은 양수를 의미한다; epsilon)이 성립하면 𝑓 '(𝒙₁) ≈ 0 이 되어 (우리가 허용하는 오차범위에서) 임계점 정리를 만족하므로 알고리즘을 멈추고 𝒙₁ 을 최적인 근사해로 반환한다.
그러나 |𝒈₁| > ɛ 이면 계산공식 𝒙₂ = 𝒙₁ - 𝜂𝒈₁ 을 이용하여 𝒙₂ 를 결정한다. 같은 방법으로 𝒈₂ = 𝑓 '(𝒙₂) 를 계산하여 임계점 정리를 만족하는지 판단해보고, 만일 성립되지 않으면 𝒙₃ 를 결정한다. 이런 방식으로 𝒙₄, 𝒙₅, … (→𝒙*)를 만들어 낸다.
아래 그림과 같이 𝒌번째 단계의 근사해 𝒙𝒌에서의 접선의 기울기가 𝐠𝒌 = 𝑓 '(𝒙𝒌) < 0 을 만족한다고 하자. 그러면 𝒙𝒌 에서 오른쪽으로(양의 방향) 이동할 때 함수가 감소하므로 최솟값을 갖는 최적해 𝒙*는 𝒙𝒌 의 오른쪽에 있다고 판단할 수 있다. 따라서 𝒙𝒌에서 -𝐠𝒌(>0) 방향(오른쪽)으로 이동하여 𝒙𝒌﹢₁ = 𝒙𝒌 - 𝜂𝒈𝒌 을 생성한다.

마찬가지로 아래 그림과 같이 𝒌번째 단계의 근사해 𝒙𝒌에서의 접선의 기울기가 𝐠𝒌 = 𝑓 '(𝒙𝒌) > 0 을 만족한다고 하자. 그러면 𝒙𝒌 에서 왼쪽으로(음의 방향) 이동할 때 함수가 감소하므로 최솟값을 갖는 최적해 𝒙*는 𝒙𝒌 의 왼쪽에 있다고 판단할 수 있다. 따라서 𝒙𝒌에서 -𝐠𝒌(<0) 방향(왼쪽)으로 이동하여 𝒙𝒌﹢₁ = 𝒙𝒌 - 𝜂𝒈𝒌 을 생성한다.

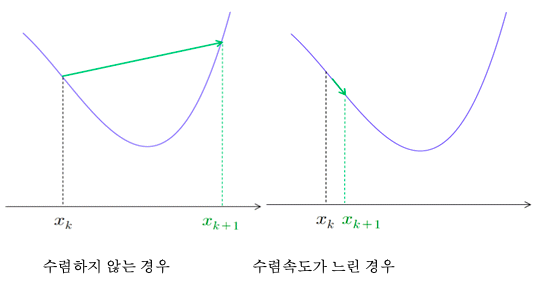
이를 통해 경사하강법은 𝑓(𝒙₁) > 𝑓(𝒙₂) > 𝑓(𝒙₃) … 가 만족되도록 𝒙₁, 𝒙₂, 𝒙₃, … 을 찾으려고 하는 것임을 알 수 있다. 이때 얼마만큼을 이동해야 하는지는 𝜂 (eta)가 결정하는데, 이를 학습률(learning rate)이라고 한다. 학습률이 너무 크면 𝒙*를 넘어서 지나칠 수 있고, 심지어 함수값이 증가하여 수렴하지 않을 수도 있다(아래 왼쪽 그림). 반대로 너무 작으면 수렴하는 속도가 느릴 수 있다(아래 오른쪽 그림).
[참고]
적절한 학습률을 결정하는 것은 경사하강법에서 중요한 문제이나 여기서는 자세히 다루지 않는다. 학습률은 대개 10⁻⁶ 에서 1 사이의 범위에서 정하는 것으로 알려져 있으며, 초기 학습률로는 𝜂 = 0.1 또는 𝜂 = 00.1 이 주로 사용된다고 한다.
예제 1. 함수 𝑓(𝒙) = 2𝒙² - 3𝒙 +2 의 최솟값을 구하시오. 단, 𝒙₁ = 0, 𝜂 = 0.1, 𝒆 = 10⁻⁶ 으로 한다.
풀이) 𝑓 '(𝒙) = 4𝒙 -3 = 0 에서 임계점은 𝒙 = ¾ = 0.75 이고 𝑓(𝒙) 는 아래로 볼록한 이차함수이므로 𝒙 = ¾ 에서 최솟값 𝑓(¾) = ⅞ 임을 쉽게 알 수 있다.
f(x) = 2*x^2 - 3*x + 2 # 함수
df(x) = diff(f(x), x) # 도함수
x0 = 0.0 # 초기 근사해
tol = 1e-6 # 허용오차
eta = 0.1 # 학습률
for k in range(300):
g0 = df(x0)
if abs(g0) <= tol:
print("알고리즘 성공!")
break
x0 = x0 - eta*g0
print("x* =", x0)
print("|g*| =", abs(g0))
print("f(x*) =", f(x0))
print("반복 횟수 =", k + 1)
알고리즘 성공!
x* = 0.749999834194560
|g*| = 6.63221759289456e-7
f(x*) = 0.875000000000055
반복 횟수 = 31
위의 예제에서 경사하강법에 의해 생성된 점들 (𝒙₁, 𝑓(𝒙₁)), (𝒙₂, 𝑓(𝒙₂)), (𝒙₃, 𝑓(𝒙₃)), … 을 함수 𝐲 = 𝑓(𝒙) 의 그래프와 함께 좌표평면에 나타내면 다음과 같다. 그림을 통해 직관적으로 최솟값을 가지는 곡선위의 점 (𝒙*, 𝑓(𝒙*)) 에 수렴함을 쉽게 알 수 있다.

경사하강법은 딥러닝에서 가중치를 업데이트하는 데 사용되는 핵심 알고리즘이기도 하다. 앞서 경사하강법을 소개할 때 정의역 전체에서 아래로 볼록(convex)인 함수를 가정하였다. 그러나 구간마다 아래로 볼록, 위로 볼록이 모두 포함된 함수(non-convex, 예. 아래 그림)에 경사하강법을 적용하면, 시작점 𝒙₁ 이 어디냐에 따라 서로 다른 극솟값 또는 (극대도 극소도 아닌) 임계점으로 수렴할 수도 있다.

✔︎ 응용(최소제곱문제)
최소제곱문제도 역시 경사하강법으로 해결할 수 있다.
min 𝑬(u)
다만 앞서 소개한 경사하강법은 독립변수가 하나인 일변수 함수 𝑓(𝒙)에 대하여 구성하였는데, 우리가 학습한 최소제곱문제는 독립변수가 최소 2개 이상인 다변수 함수 𝑬(u) 이므로 다음과 같이 변형된다.
[알고리즘]

다변수 함수에 대한 경사하강법도 기본적인 구성은 일변수 함수의 경우와 완전히 같으나 스칼라 𝒙 가 벡터 u로, 절대값 |𝐠| 가 벡터의 노름 ||𝐠|| 으로, 도함수 𝑓 '(𝒙) 가 (다변수함수에서 도함수 역할을 하는) 그래디언트(gradient) ∇𝑬(u) 로 바뀌는 것만 차이가 있다.
𝒙, 𝐲 를 독립적으로 변화하는 두 변수라 하고 𝐳 를 제 3의 변수라 하자. 𝒙, 𝐲 의 값이 각각 정해지면 여기에 대응하여 𝐳 의 값이 정해질 때 𝐳 를 두 변수 𝒙, 𝐲 의 함수라 하고 이것을 𝐳 = 𝑓(𝒙, 𝐲) 로 표시한다. 같은 방법으로 더 많은 변수의 함수도 정의할 수 있다. 이와 같이 이변수 이상의 함수를 일반적으로 다변수함수라 한다.
좌표 공간에서 𝒙, 𝐲 및 𝐳 = 𝑓(𝒙, 𝐲) 를 좌표로 하는 점 (𝒙, 𝐲, 𝐳)를 생각하고 𝒙, 𝐲를 움직이면 그들 점은 일반적으로 하나의 곡면을 이루게 되는데 이 곡면을 함수 𝐳 = 𝑓(𝒙, 𝐲) 의 그래프라 부른다.

var('x, y') # 변수 정의
f(x, y) = -x*y*exp(-x^2 - y^2)
plot3d(f(x, y), (x, -2, 2), (y, -2, 2), opacity = 0.6, aspect_ratio = [1, 1, 10])
위의 그래프에서 산의 정상에 해당하는 부분에서 이변수 함수는 극댓값을 갖게 되고, 계곡의 바닥에 해당하는 부분에서 극솟값을 갖게 됨을 직관적으로 확인할 수 있다. 이 점을 찾기 위해서는 일변수 함수의 도함수에 해당하는 개념이 필요하다. 이를 다변수 함수의 그래디언트(gradient)라고 한다.
✔︎ 다변수 함수의 도함수(그래디언트)
이변수 함수 𝑓(𝒙, 𝐲) 의 그래디언트는 다음과 같이 정의된다.

여기서 𝜕𝑓 / 𝜕𝒙 는 𝑓 를 변수 𝒙 에 관하여 편미분한다는 뜻으로 𝒙 를 제외한 다른 변수는 모두 상수로 취급하여 미분하는 것과 같다.

var('x, y') # 변수 정의
f(x, y) = -x*y*exp(-x^2 - y^2)
f(x, y).gradient() # 그래디언트(2*x^2*y*e^(-x^2 - y^2) - y*e^(-x^2 - y^2), 2*x*y^2*e^(-x^2 - y^2) - x*e^(-x^2 - y^2))
같은 방법으로 독립변수가 3개 이상인 다변수함수 𝑓 에 대하여도 𝑓 의 그래디언트를 정의할 수 있다. 𝜂 변수 함수 𝑓(𝒙₁, 𝒙₂, …, 𝒙𝘯) 에 대하여 그래디언트는 다음과 같다.


각 데이터 (𝒙ᵢ, 𝐲ᵢ)에 대하여 𝒙ᵢ를 일차함수 𝐲 = a + b𝒙 에 대입하여 얻은 값을 ŷᵢ 라 하자(즉 ŷᵢ = a + b𝒙ᵢ). 이 선형연립방정식의 해가 존재하지 않는 경우. 각 데이터와 근사식 사이의 (제곱)오차 (𝐲ᵢ - ŷᵢ)² 가 최소가 되는 a, b를 구하기 위하여 각 데이터에 대하여 오차(error)를 더한 오차함수는 다음과 같다. (앞에 ½ 은 단지 계산의 편리성을 주기 위해서 곱해주었다.)

이에 대하여 경사하강법을 사용하면 다음을 얻는다. (u = (1, 1), 허용오차 ɛ = 10⁻⁶, 학습률 𝜂 = 0.1)
var('a, b') # 변수 선언
# 오차함수
E(a, b) = 1/2*((a - 1)^2 + (a + b - 3)^2 + (a + 2*b - 4)^2 + (a + 3*b - 4)^2)
# 도함수(그래디언트)
gradE = E.gradient()
u = vector([1.0, 1.0]) # 초기 근사해
tol = 1e-6 # 허용오차 10^(-6)
eta = 0.1 # 학습률(learning rate)
for k in range(300):
g = gradE(u[0], u[1])
gn = g.norm()
if gn <= tol:
print("알고리즘 성공 !")
break
u = u - eta*g
print("u* =", u)
print("E(x*) =", E(u[0], u[1]))
print("반복 횟수 =", k + 1)
알고리즘 성공 !
u* = (1.49999931357138, 1.00000032150597)
E(x*) = 0.500000000000342
반복 횟수 = 106
따라서 최소제곱직선은 𝐲 = 3/2 + 𝒙 이다.


마찬가지로 𝒙, 𝐲 관계를 가장 잘 보여주는 이차식 𝐲 = a + b𝒙 + c𝒙² 도 찾을 수 있다. 오차는 다음과 같다.

역시 경사하강법을 사용하면 아래의 이차함수 𝐲 = a + b𝒙 + c𝒙² 을 얻는다. (u = (1, 1, 1), 허용오차 ɛ = 10⁻⁶, 학습률 𝜂 = 0.01)
var('a, b, c') # 변수 선언
# 오차함수
E(a, b, c) = 1/2*((a - 1)^2 + (a + b + c - 3)^2 + (a + 2*b + 4*c - 4)^2 + (a + 3*b + 9*c - 4)^2)
# 도함수(그래디언트)
gradE = E.gradient()
u = vector([1.0, 1.0, 1.0]) # 초기 근사해
tol = 1e-6 # 허용오차 10^(-6)
eta = 0.01 # 학습률(learning rate)
for k in range(5000):
g = gradE(u[0], u[1], u[2])
gn = g.norm()
if gn <= tol:
print("알고리즘 성공!")
break
u = u - eta*g
print("u* =", u)
print("E(x*) =", E(u[0], u[1], u[2]))
print("반복 횟수 =", k + 1)알고리즘 성공!
u* = (1.00000138155249, 2.49999723768073, -0.499999180018564)
E(x*) = 1.59664737265671e-12
반복 횟수 = 4207
즉, 이차함수 𝐲 = a + b𝒙 + c𝒙² 의 계수가 a = 1, b = 2.3, c = -0.5 이므로, 최소제곱곡선은 𝐲 = 1 + 5/2𝒙 - 1/2𝒙² 이다.

'◦ Machine Learning > Mathmatics' 카테고리의 다른 글
| [기초수학] 순열과 조합, 확률, 확률변수, 확률분포, 베이지안 (0) | 2021.01.17 |
|---|---|
| [기초수학] 극대, 극소, 최대, 최소 (0) | 2021.01.11 |
| [기초수학] 극한과 도함수 (0) | 2021.01.11 |
| [기초수학] 정사영과 최소제곱문제 (0) | 2021.01.09 |
| [기초수학] 선형연립방정식의 해집합 (0) | 2021.01.08 |